A PCA biplot is a specific type of biplot created using Principal Component Analysis (PCA).
In this PCA with python tutorial, we will learn how to plot a 2D and a 3D biplot in Python using Scikit-learn and PCA
A PCA biplot in Python combines the scatter plot of the PCA scores and loading plots to show how data points relate to each other.
This visualization helps in data analysis and machine learning to understand the structure of the data, identify patterns, and observe the relationships between variables.
The PCA Biplot is one of the PCA visualization techniques used in dimensionality reduction.
How to Make a PCA 2D Biplots in Python?
To visualize a 2D Biplot, you will first need to create a loading plot and a scatter plot of the PCA data, and then combine them to each other.
A Biplot is a graphs that shows:
- the scaled PCA scatterplots
- the loading plots in addition
- vectors that show how strongly each feature influences the principal component.
What is a Loading Plot?
A PCA loading plot in Python helps to visualize how original features contribute to the principal components to understand which variables have the most influence on the transformed data.
The loading plot shows vectors starting from the origin to the loadings of each feature.
The loadings (or weights) are the correlation coefficients between the original features and the principal components.
They represent the elements of the eigenvector.
Squared loadings of the principal components are always equal to 1.
The loadings can be accessed using pca.components_.
Inspired by Renesh Bedre, I will create a loading plot to help understand what they are.
How to Make a PCA Loading Plot in Python
To make a PCA loading plot in Python, we first reduce the dataset using PCA and the we plot the correlation coefficients of each feature / principal component.
Follow this tutorial to understand how to perform PCA with Python.
Create Correlation Coefficients Dataframe in Python
To understand how each feature impact each principal component (PC), we will show the correlation between the features and the principal components created with PCA.
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import pandas as pd
# load features and targets separately
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Scale Data
x_scaled = StandardScaler().fit_transform(X)
# Perform PCA on Scaled Data
pca = PCA(n_components=2)
pca_features = pca.fit_transform(x_scaled)
# Principal components correlation coefficients
loadings = pca.components_
# Number of features before PCA
n_features = pca.n_features_in_
# Feature names before PCA
feature_names = iris.feature_names
# PC names
pc_list = [f'PC{i}' for i in list(range(1, n_features + 1))]
# Match PC names to loadings
pc_loadings = dict(zip(pc_list, loadings))
# Matrix of corr coefs between feature names and PCs
loadings_df = pd.DataFrame.from_dict(pc_loadings)
loadings_df['feature_names'] = feature_names
loadings_df = loadings_df.set_index('feature_names')
loadings_df
The result is a dataframe with the loadings (correlation coefficients).
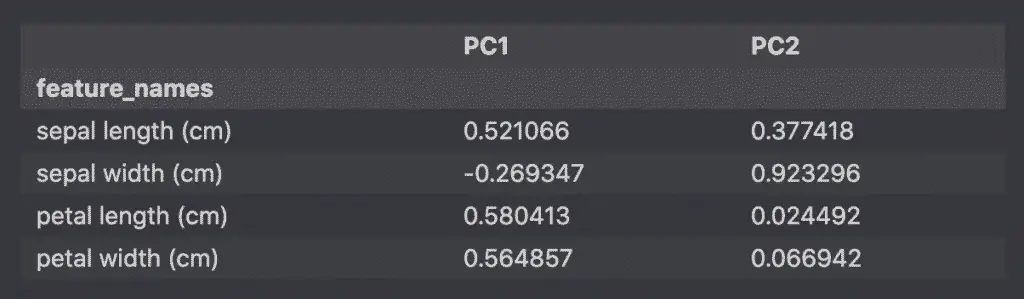
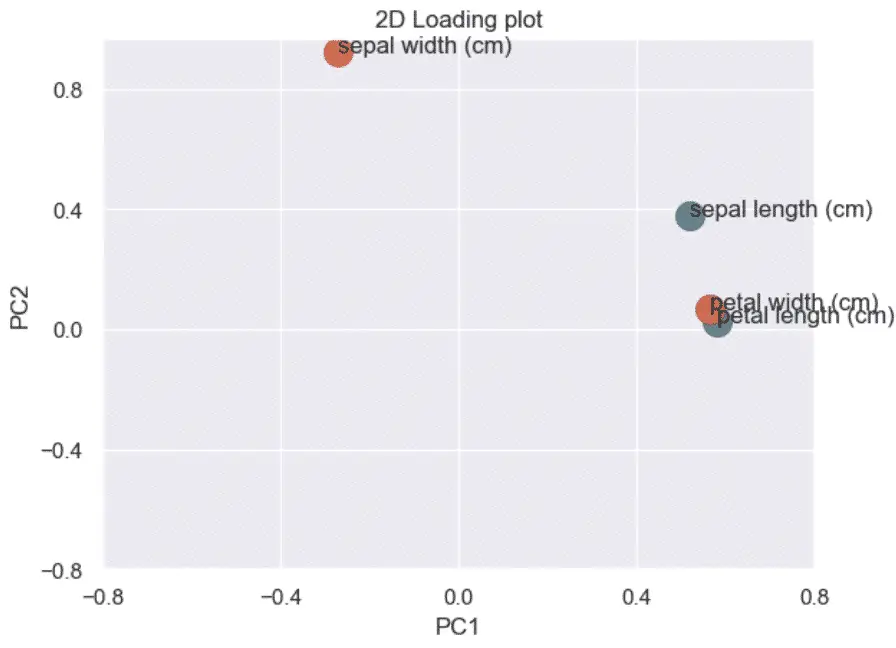
How to make a 2D loading plot in Python
The loading plot helps understand which features impact which principal component and by how much.
First, we plot the correlation coefficients (loadings) of each feature.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
sns.set()
# Get the loadings of x and y axes
xs = loadings[0]
ys = loadings[1]
# Plot the loadings on a scatterplot
for i, varnames in enumerate(feature_names):
plt.scatter(xs[i], ys[i], s=200)
plt.text(xs[i], ys[i], varnames)
# Define the axes
xticks = np.linspace(-0.8, 0.8, num=5)
yticks = np.linspace(-0.8, 0.8, num=5)
plt.xticks(xticks)
plt.yticks(yticks)
plt.xlabel('PC1')
plt.ylabel('PC2')
# Show plot
plt.title('2D Loading plot')
plt.show()
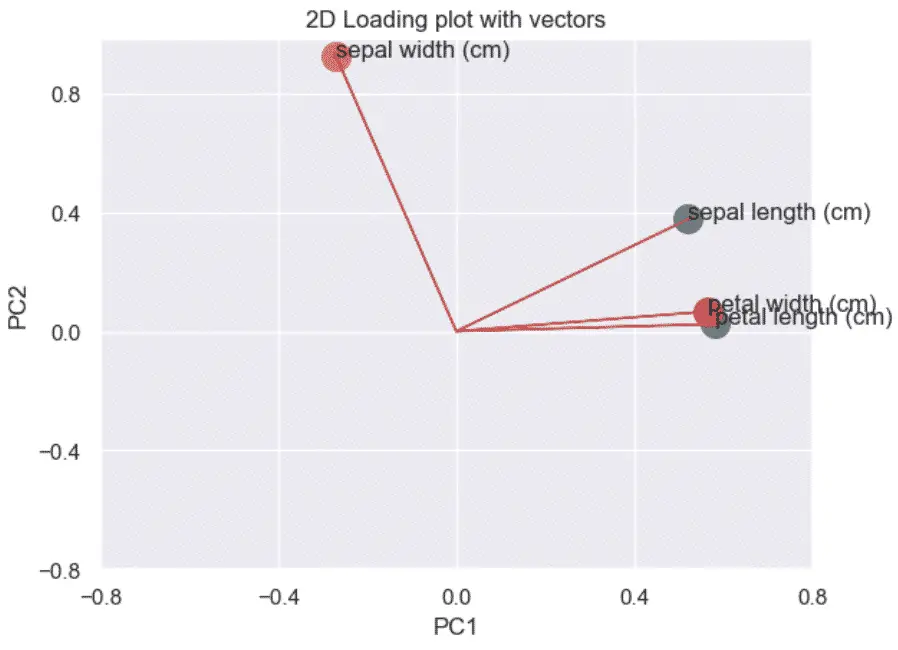
Then, we plot the directionality of the correlation by adding arrows from the origin (0, 0) to each of the coefficients.
import matplotlib.pyplot as plt
import numpy as np
# Get the loadings of x and y axes
xs = loadings[0]
ys = loadings[1]
# Plot the loadings on a scatterplot
for i, varnames in enumerate(feature_names):
plt.scatter(xs[i], ys[i], s=200)
plt.arrow(
0, 0, # coordinates of arrow base
xs[i], # length of the arrow along x
ys[i], # length of the arrow along y
color='r',
head_width=0.01
)
plt.text(xs[i], ys[i], varnames)
# Define the axes
xticks = np.linspace(-0.8, 0.8, num=5)
yticks = np.linspace(-0.8, 0.8, num=5)
plt.xticks(xticks)
plt.yticks(yticks)
plt.xlabel('PC1')
plt.ylabel('PC2')
# Show plot
plt.title('2D Loading plot with vectors')
plt.show()
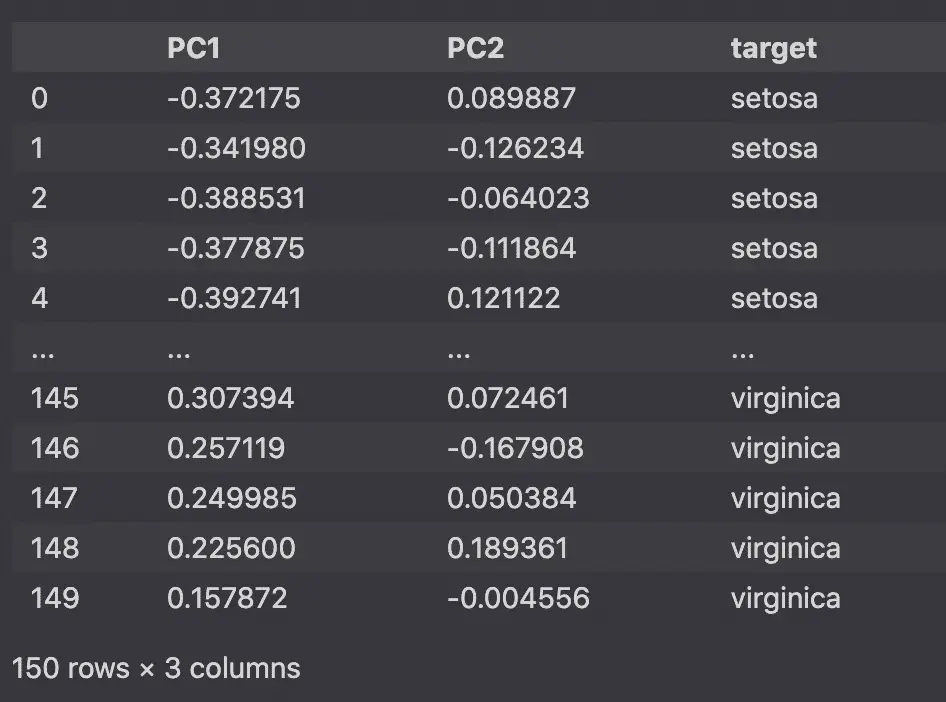
Scale the PCA data with Python
We will scale the PCA plot again to plot it against the loading plots.
I have borrowed some of the code below from Prasad Ostwal‘s fantastic tutorial on PCA.
# Create DataFrame from PCA
pca_df = pd.DataFrame(
data=pca_features,
columns=['PC1', 'PC2'])
# Map Targets to names
target_names = {
0:'setosa',
1:'versicolor',
2:'virginica'
}
pca_df['target'] = y
pca_df['target'] = pca_df['target'].map(target_names)
# Scale PCS into a DataFrame
pca_df_scaled = pca_df.copy()
scaler_df = pca_df[['PC1', 'PC2']]
scaler = 1 / (scaler_df.max() - scaler_df.min())
for index in scaler.index:
pca_df_scaled[index] *= scaler[index]
pca_df_scaled
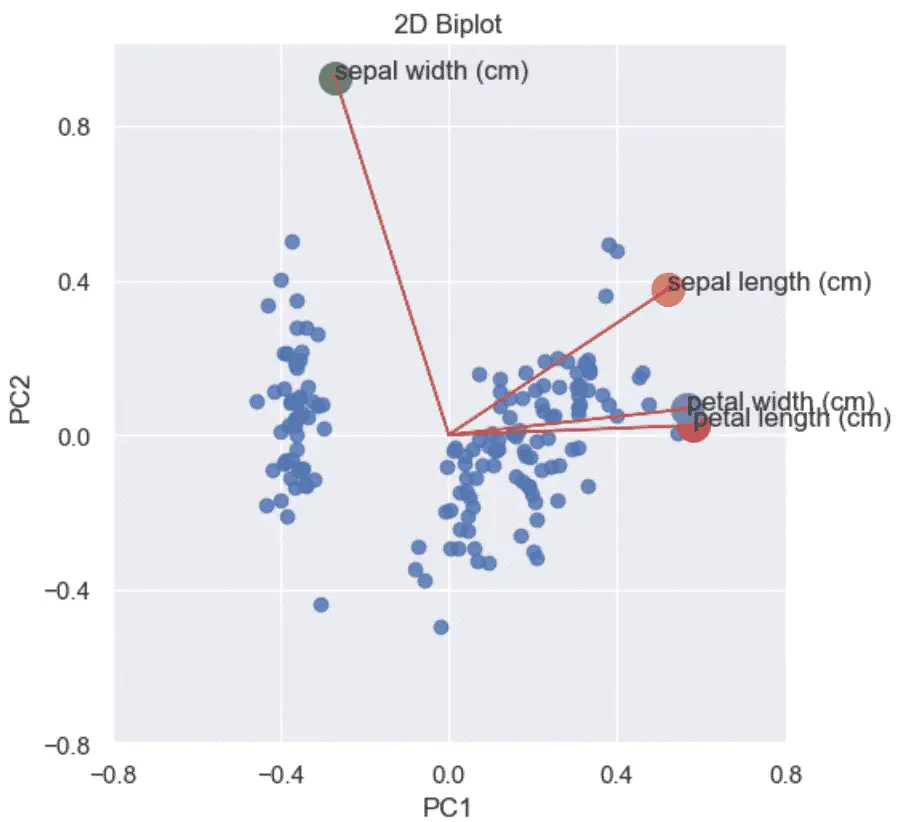
Combine the Scatterplot and the Loading plot into a Biplot
Using the loading plots and the scaled plots we can now show the correlation coefficients against the PCA scatterplot on the same graph.
# 2D
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
xs = loadings[0]
ys = loadings[1]
sns.lmplot(
x='PC1',
y='PC2',
data=pca_df_scaled,
fit_reg=False,
)
for i, varnames in enumerate(feature_names):
plt.scatter(xs[i], ys[i], s=200)
plt.arrow(
0, 0, # coordinates of arrow base
xs[i], # length of the arrow along x
ys[i], # length of the arrow along y
color='r',
head_width=0.01
)
plt.text(xs[i], ys[i], varnames)
xticks = np.linspace(-0.8, 0.8, num=5)
yticks = np.linspace(-0.8, 0.8, num=5)
plt.xticks(xticks)
plt.yticks(yticks)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('2D PCA Biplot (Python)')
plt.show()
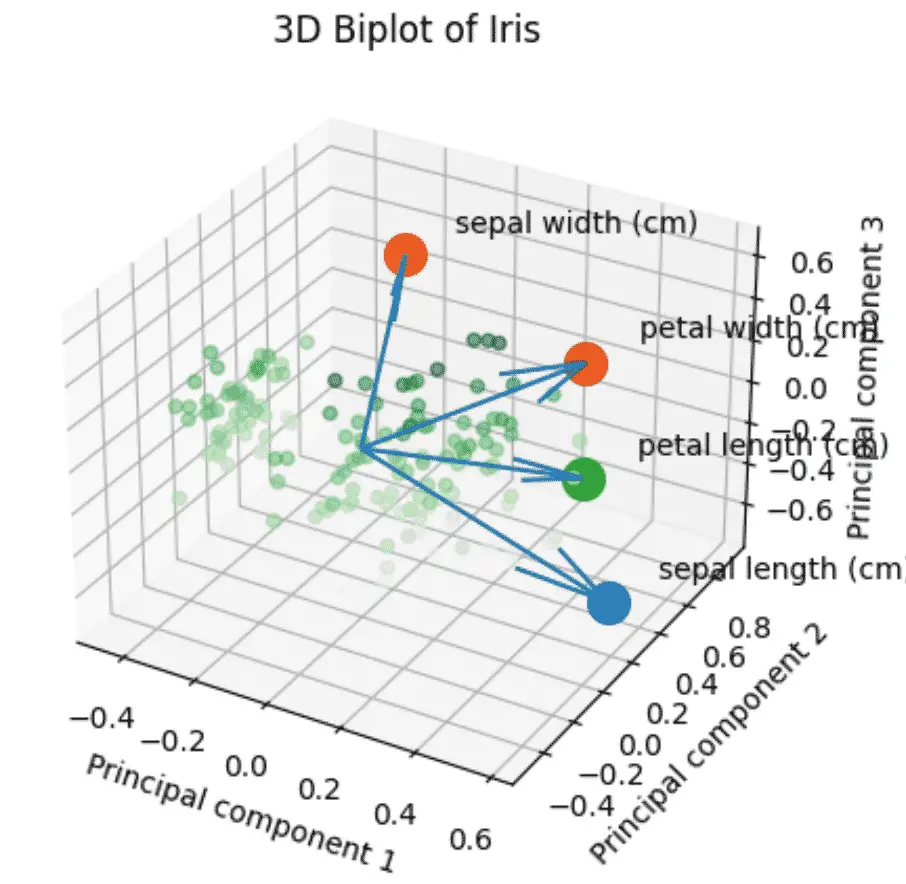
How to make a PCA 3D Biplots in Python?
The PCA 3D biplot combines all the steps above using 3 components instead of 2.
This Python code is about using Principal Component Analysis (PCA) to reduce the dimensions of data and then visualizing it in a 3D biplot.
It takes the input data from the Iris Dataset, applies StandardScaler and PCA to it, and creates a 3D scatterplot with the transformed data points.
- Data points are colored based on their position in the third component.
- Original features’ contributions are displayed as arrows.
The PCA 3D biplot helps to understand relationships between data points and features in a 3D space.
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
plt.style.use('default')
# load features and targets separately
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Scale Data
x_scaled = StandardScaler().fit_transform(X)
pca = PCA(n_components=3)
# Fit and transform data
pca_features = pca.fit_transform(x_scaled)
# Create dataframe
pca_df = pd.DataFrame(
data=pca_features,
columns=['PC1', 'PC2', 'PC3'])
# map target names to PCA features
target_names = {
0:'setosa',
1:'versicolor',
2:'virginica'
}
# Apply the target names
pca_df['target'] = iris.target
pca_df['target'] = pca_df['target'].map(target_names)
# Feature names before PCA
feature_names = iris.feature_names
# Create the scaled PCA dataframe
pca_df_scaled = pca_df.copy()
scaler_df = pca_df[['PC1', 'PC2', 'PC3']]
scaler = 1 / (scaler_df.max() - scaler_df.min())
for index in scaler.index:
pca_df_scaled[index] *= scaler[index]
# Initialize the 3D graph
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Define scaled features as arrays
xdata = pca_df_scaled['PC1']
ydata = pca_df_scaled['PC2']
zdata = pca_df_scaled['PC3']
# Plot 3D scatterplot of PCA
ax.scatter3D(
xdata,
ydata,
zdata,
c=zdata,
cmap='Greens',
alpha=0.5)
# Define the x, y, z variables
loadings = pca.components_
xs = loadings[0]
ys = loadings[1]
zs = loadings[2]
# Plot the loadings
for i, varnames in enumerate(feature_names):
ax.scatter(xs[i], ys[i], zs[i], s=200)
ax.text(
xs[i] + 0.1,
ys[i] + 0.1,
zs[i] + 0.1,
varnames)
# Plot the arrows
x_arr = np.zeros(len(loadings[0]))
y_arr = z_arr = x_arr
ax.quiver(x_arr, y_arr, z_arr, xs, ys, zs)
# Plot title of graph
plt.title(f'3D Biplot of Iris')
# Plot x, y, z labels
ax.set_xlabel('Principal component 1', rotation=150)
ax.set_ylabel('Principal component 2')
ax.set_zlabel('Principal component 3', rotation=60)
plt.show()
Conclusion
We now have learn how to make Principal Component Analysis 2D and 3D biplots in Python to understand the structure of the data, see you soon!

SEO Strategist at Tripadvisor, ex- Seek (Melbourne, Australia). Specialized in technical SEO. Writer in Python, Information Retrieval, SEO and machine learning. Guest author at SearchEngineJournal, SearchEngineLand and OnCrawl.
