What is Causal Impact Analysis and How to Use it?

In this introduction, you will understand what is CausalImpact and how it can be used. Causal Impact is a package used to understand the causal effect of an event in the absence of an experiment.

What is CausalImpact?

CausalImpact is a package created by Kay H. Brodersen that uses Bayesian statistics to infer the causal effect of an event.

It is commonly used in pre-post experiments or to evaluate the effect of a past event.

How CausalImpact Works?

CausalImpact (CI) uses predictive analytics to estimate what would have happened to a variable in the absence of an event, also known as causal inference.

Then, it compares the actual results to the estimation.

In other words, it tries to estimate the counterfactual and compare it to the observations.

What Causal Impact can be used for?

Causal can be used in multiple contexts:

• SEO Experiments
• Marketing and advertising campaigns
• Stock Market analysis

Different Types of CausalImpact Experiments

1. Simple pre-post experiments
2. Experiments using control groups

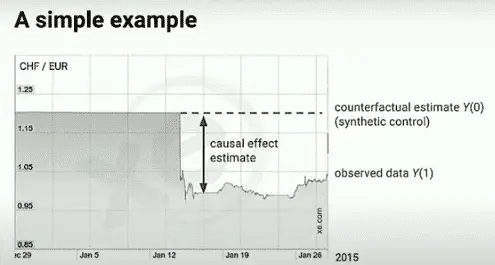
Simple pre-post experiments

CausalImpact can be used with a single dataset (y) without any control group.

In which case, using seasonality and other factors, Causalimpact will make a prediction based on previously observed data in the absence of an event.

Then, it will compare the actual observation to the predicted data.

Experiments using control groups

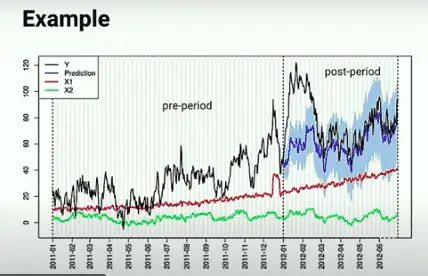
CausalImpact can be used with a test dataset (y) with 1 or multiple control groups (X1, X2, …, Xn).

In this case, it will use the control groups to try to make a better estimation of the data in the absence of the event.

---

Test groups vs control groups

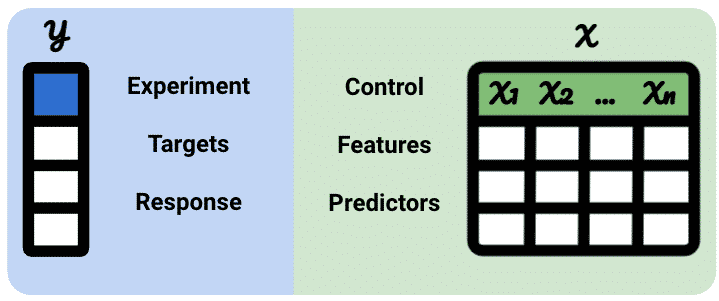
Control groups are datasets that are not impacted by an event. They can be used to improve the prediction of your test data. In other words, is the group that didn’t have an event.

Test group is the dataset that was impacted by an event. This is what you want to measure.

Control groups can be different things:

1. Independent data such as search trends of a topic in Google Trends
2. Different market data
3. Subsection of a market
4. and more

By convention, the test group is usually labelled as y and the control groups as X.

---

How to use CausalImpact With Python or R

Below are two tutorials to help use CausalImpact in R (original package) or Python (wrapper).

• SEO Experiment with CausalImpact and R
• SEO Experiment with CausalImpact and Python

---

Intepret the CausalImpact Graph

Regardless of the style applied to your graphs, it should look something like this.

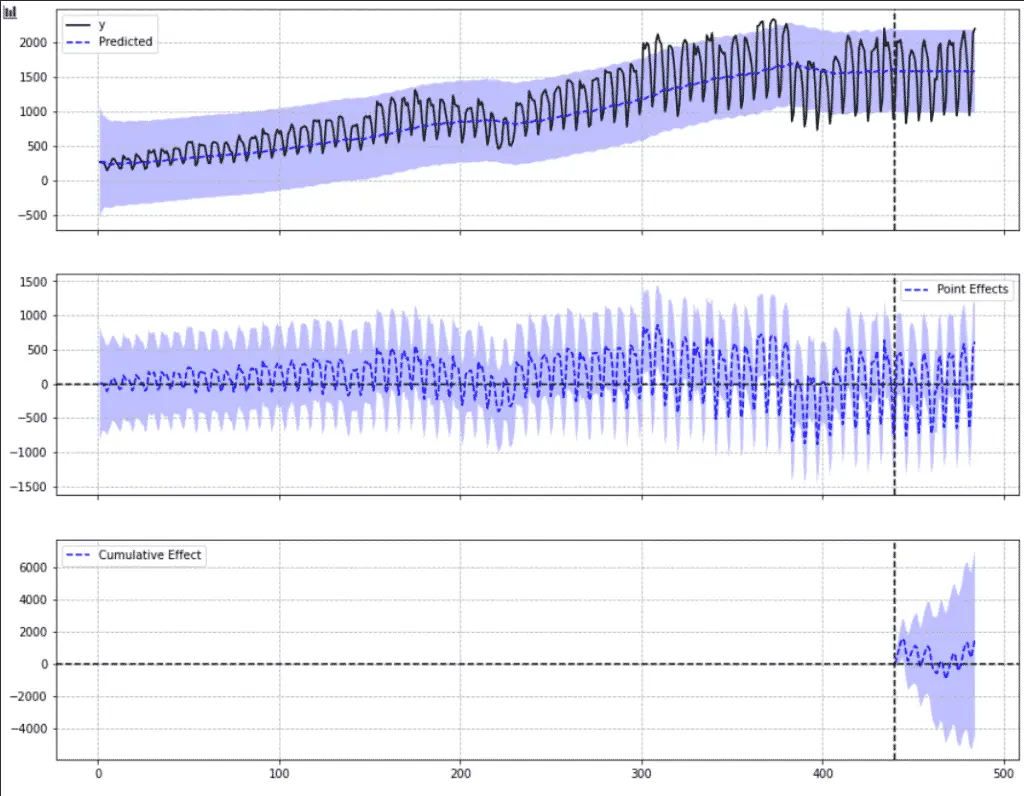
In the graph above:

• the vertical dotted line represents the intervention date
• The 0 dotted line represents the boundary where above means positive variations and below negative variations.
• The shaded area represents the confidence interval.

The top graph shows the observed data against the predicted values.

The middle graph shows the point effect of one against each other

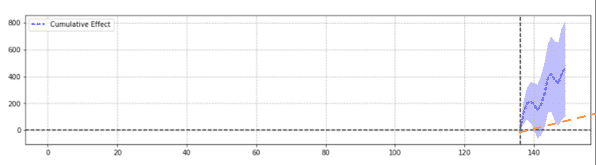
The bottom graph shows the cumulative effect of the confidence interval.

Statistical Significance

Given a 95% confidence interval, Causal Impact will tell you whether your experiment is statistically significant.

In the graph, statistical significance is reached whenever the shaded area goes above or below the 0 lines (like in the example below).

---

How Precise is Causal Impact?

Causal Impact can be very precise, but can also be quite wrong.

The quality of the model is dependent on the data it is given.

I have written an in-depth article on OnCrawl to show how to evaluate the quality of Causal Impact experiments by using the loss function.

Evaluating The Quality Of CausalImpact Predictions

Science Behind CausalImpact

Citations

CausalImpact Package Documentation

CausalImpact Essay

Conclusion

In this gentle introduction to Causal Impact, we have learned the basics of what is, how it works and how to interpret its results. Next, I would suggest that you read the official documentation to get a broader understanding of how you can use it.