The PCA machine algorithm works by identifying the intrinsic dimension of a dataset, while retaining as much variation as possible.
In other words, it identifies the smallest number of features required to make an accurate prediction.
To do so, it reduces multicollinearity by determining a new coordinate system using linearly independent orthogonal axes (Perpendicular).
The goal is to transform correlated features into orthogonal (uncorrelated) components, thus reducing dimensions and end-up with uncorrelated axes.
It uses the concept of eigendecomposition to decompose a covariance matrix into eigenvalues and eigenvectors.
Next, it finds the variance of the data into the uncorrelated axes and select the N eigenvectors with the highest eigenvalues.
Finally, it discards the eigenvectors of lowest variance.
A dataset may have a lot of features, but not all features are essential to the prediction.
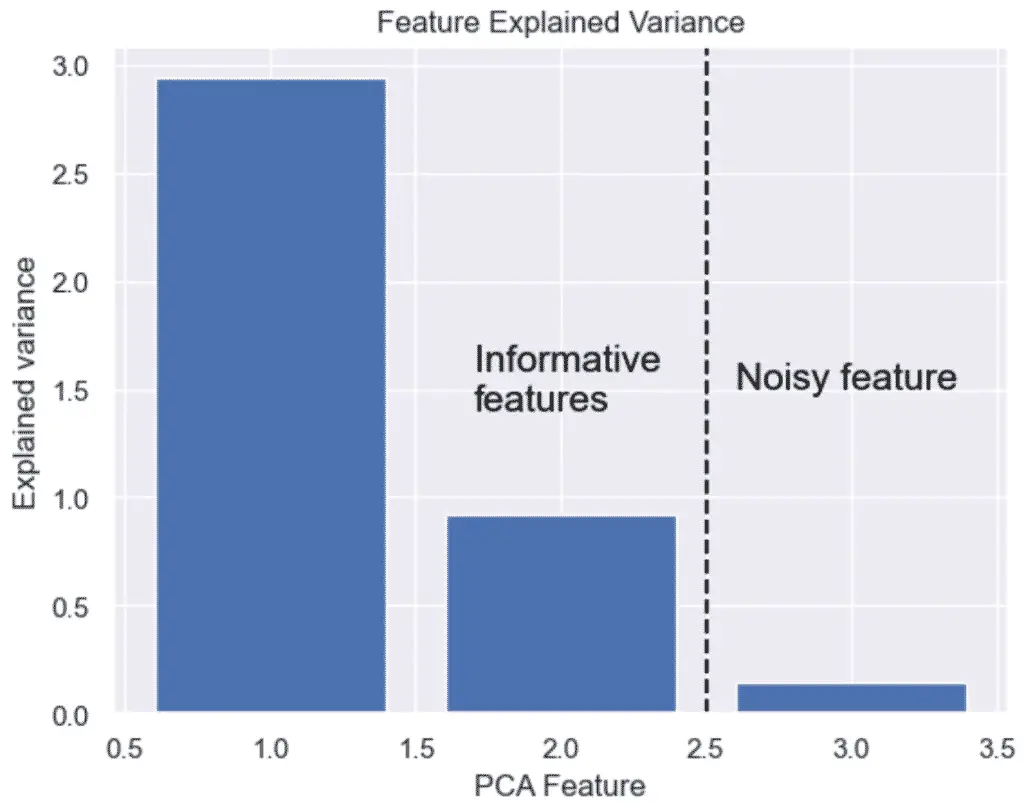
The features kept are the ones that have significant variance.
- The linear mapping of the data to a lower-dimensional space is performed in a way that maximizes the variance of the data.
- PCA assumes that features with low variance are irrelevant and features with high variance are informative.
Read the following tutorial to learn more about how to perform PCA in Python.

SEO Strategist at Tripadvisor, ex- Seek (Melbourne, Australia). Specialized in technical SEO. Writer in Python, Information Retrieval, SEO and machine learning. Guest author at SearchEngineJournal, SearchEngineLand and OnCrawl.